Morning Met and Pinkwallers,
It’s too early fi Bobette a pop up pan mi time line and mi and ar is of no friends but look pan di caption to nuh bout sorry for LOST. Lady guh have a seat ya because we naw lose nuttin a you a lose guh learn the difference between lost and loss and stop model inna brand and caay even construct a sentence….
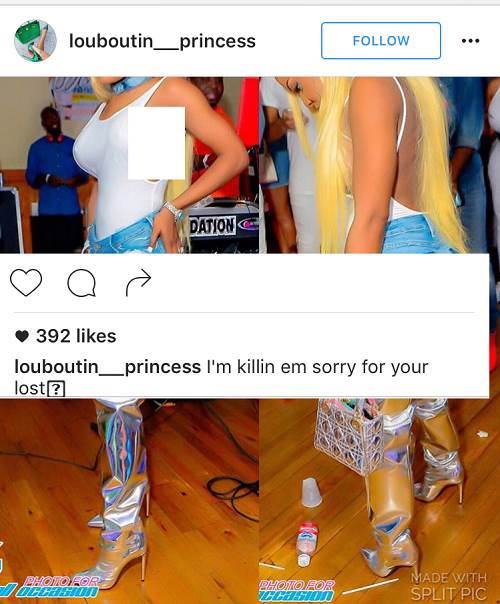
Honestly she look like sunday morning carrot,fe a slim girl.The silicon dem give r big top and Lil bottom.
Dwfl I knew this would reach up here today….just saw it scrolling through IG ….smh
Wanna be Apple so bad
I just wanna know who ia the rightful owner of the shoes because I seen Apple in them
This too shall “past” yaw robbi
Those boots are ugly….i don’t care if they cost a million dollars! Tackkkyyyyyyy!!!!!!!
bitch look like the tin man’s slutty sister, the tin ma’am
Senda no Man U read wrong she meant sorry to the store who LOST their shoes in her bag a dat she mean man
:hammer
Sender u just a hater
Hate yu mumma fi birth yu crotches! Move from ova yah wid yu hater phuckry!
This rat can’t lost ina zinc when a it use to be har crib, gate, chimmy, stove an house. She going to be list in steel bars one day one day.
Same suh :ngakak :ngakak
Choot woieeeeee :ngakak :ngakak :ngakak :ngakak :ngakak
Still can’t get over the fact that she jacked a 2year old style lol
Di only ting she need fi sorry weh lost is the time weh she ah guh spend inna lock up when dem hold har claat fi thiefT. Guh thiefT a dictionary gyal.