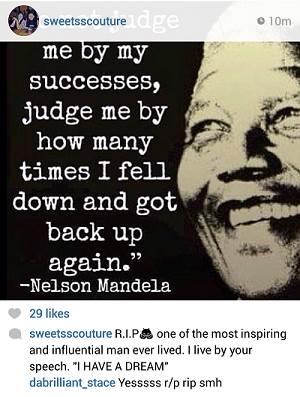
First of let me pay my respect to the late Sir Nelson Mandela. May you Sleep in Eternal Peace. Now u miss Sweets, you claim ur in college rite,so how u make a post like this? No bother say it was an error cuz if u did know ur black history u would’ve known it was the great Martin Luther King Jr who wrote that speech. Sweets I have a dream that one day u will gain some knowledge and stop being a dunce.
but a weh di bloodclawt :tkp
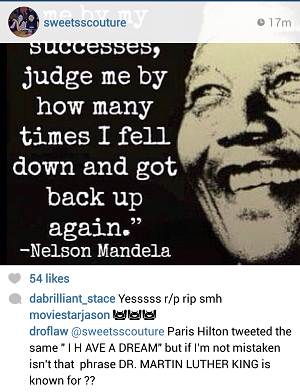
up to Paris Hilton seh dis same fuxxery…a doah noe who betta smh
A wha di rass…………
Social networks will be the death of these people. My goodness.
To laugh often and love much; to win the respect of intelligent persons and the affection of children; to earn the approbation of honest citizens and endure the betrayal of false friends; to appreciate beauty; to find the best in others; to give of one’s self; to leave the world a bit better, whether by a healthy child, a garden patch or a redeemed social condition; to have played and laughed with enthusiasm and sung with exultation; to know even one life has breathed easier because you have lived—this is to have succeeded.
Di white people dem ina one piece a upsetment because people see mandela as a hero ..one a dem comment pan an article a hint towards the end of aparthide mek south africa poor so it is really a shame when black people nuh know we history
mi just sorry say dem tek whey so much time from him and old age get the best a him. dem a cheer now but when china move in pon dem rass dem i see
Dem know BLEACH history! Ask dem which one go wid which and which year dem start or stop mek one brand, and which one have de best strength…Dem is an insult to higher educations.
Please don’t think they are real college students cause dem enroll fi a fly-by-night course.
shame and disgrace
Dem soon create new meaning fi those two (shame and disgrace) words. lol.
I notice only KP is the brightest of all these DH “socialites”, and she should distant her self from these non-progressive, barely literate, hair-heads.
My gosh! There is NO WAY to confuse MLK with Nelson Mandela! Especially when you LIVE in America.
Even if you lived under a rock. Mi neva si dis yet …when school was happening where dem was?
sweets its DR.KING BOO i have a dream famous speech :ngakak :malu :ngakak RIP MR .nelson mandela u will be miss
You see the stupid epidemic is taking over di bleachings a nam out har brain dam fool and this is a chick these Young girls look up to a dam dunce. 😡 :cool I feel so sorry so her.
@met a true we dont know our history ..but we know every fashion the white man mekkk sad sad
f**king dunce my god smh lol tek bad things and laff sometime pretty dunce fi tru uno wasnt lying
fashionable dunce is all mi affi seh……….
Paris actually tweeted that she never made the first tweet and who ever said that was disrespectful and fake… so Sweets follows Paris and jumped on what she thought Paris said without using common sense and re tweeted what the fake Paris posted and made an ass out of her self….Not smart….
aye sahhhhhhhhh :nohope
Sweets is the scrapses/dreggs of Paris…..six of one half dozen a di odda…two dumb bitches….
Example-sweetss……dis need some sweet lemonade…..I can’t…rofl.
Poor sweets!!! I told y’all these hoes are dumb bimbos
They just say shit out their mouth cuz it make them look good
Now it caught up GREAT EVERYONE CAN NOW SEE HOW MUCH OF A DUNCE BAT YOU ARE!!!! ALL THE SPELL CHECKS DICTIONARY & HISTORY BOOKS & you STILL DONT KNOW SHIT!!!!!! Just collect your billing & coding certi sweets & the cna I leave you right there ! MLK JR LMAO u know how long him dead???? Bwoy sweets it ruff
I can imagine sweets a ask yonique ah da man yere did say I have a dream speech doh? & dolly like girl iono I think so DWL sweets puts it up anyway.. Haha!
If I laugh I poop. No man, it bad pon har. Even mi likkle 6 year old neice know sey a Martin Luther Kind did have di dream…
Sweets go and get yourself a library card and check out as many books as you can and read them. You need to be schooled from basic. SMDH!
Dumb bird bet u say she would Neva meck a mistake if given the task of selecting a brand smh poor girl it’s a pity
Lmao unno plesae leave my baby sweets alone she take down the post. She just call me and a cry.
now she a guh call yuh bak n cuss caw you cum talk oooooooooo :hammer
What a damn SHAME. Shes so stupid. But just like Class (which dem nuh have) you can’t buy common sense and intelligence. Just Shameful!! but can tell me every white mans brands out there selling. Your an embarrassment to our culture, with your bleach out skin. Which I’m sorry u will never look like a Natural Brownin, all of unno favor Walking Dead.
Hold on isnt Sweets and har Bleach sistah from Africa??????????????
they wanna b some much and follow and follow and wanna b who they r not copy fashion copy wrong info u see how dem follow and copy wrong quotes de paris she arite till di doc see she she a wesley snipe
Darling sweets a weh book do you? Read or at least google
One fool really makes many. Sweetie gal, Dr. Martin Luther King, Jr. duppy shoulda git up inna rage and plant a &^%$# bax inna yuh jawbone. Mek yuh face twist fi days!!!! I have a Dream that one day dese duncebats will one day realize dat education is de key to success. Sweets yuh want a kik right up inna yuh couture.
I Kaint Breathe…I are is deadin…DWBPCL
Mi say mi in pain mi a laff to much tidday ya man
i laaf til i weak…di post dem yasso n ova fb a kill mi…mi inna stitches :ngakak
Can I nominate dis the post of di day……Mi CHESS a hurt mi and mi side cawna….LMAO
DWLn..yu know sey Hon. Mandela have a quote pon the power of education? lolollllll
Smrch!!! So smaddy weh a look mi ask mi who name Mandela mi just tell him lose mi number and go read a book. Damn dunce dem!
Nelson Mandela does have a dream speech
yes but not a “I HAVE A DREAM” speech.
Hon. Mandela LIVED THE DREAM!
The dream you may be referring to his the one him never share and that is fi Black females fi STOP BLEACH and carry dem self like Market bag and sperm dumpstas and the for ALL BLACKS TO OBTAIN AN EDUCATION…and the man dem fi STOP being fags and sperm dumpers and criminals.
Sweets u Neva even learn a school say u Nuffi copy….sass Christ.i bet u caan even spell di bran dem wey u wear…u think pretty looks is all….go tek several f**king books in Barnes n noble….duppybat.
Ah which high school or college sweets or dolly attend? Does anybody know ?? I can bank on it that these two peas in a pod don’t own not one a dem much less a jr high school diploma di only diploma dem own a make-up; weave; clothes; shoes; suck hood; suck pussy; three sums; whorin; and still living home wid dem madda. Sweets going to fashion school doesn’t make you a college grad you will be a certificate holder ottay dummy!!
Shi did only guh Sunday school lol
all that girl know how to do is dress up party and suck pu55y go back to elementary school you dunce bat if i ever see you in the streets am pouting you out you waist of sperm.
pointing***
If me was she, mi wudda delete mi account. Everybody wants to seem deep and knowledgable , so in her quest fii gwan like she hav any depth at all, she make herself look like fool. Girl delete ur account n don’t tell nuh body u go college
When one wants to partake in intellectual conversations or make postings attributed to others they need to READ and RESEARCH. There is no excuse for this, especially from someone who purportedly is in College. This is unacceptable. A dunce move of epic proportions!!!
Tom Ford mi like you!!!! Your intelligence tun up!!!
De gal yah a d Paris Hilton fe Jamaicans Dem f**king dunce alike
All she haffi do is do what Paris did and sey it was a fake and is neva she write dat…and smaddy a try mek har look like she nah nuh sense…problem solved
On Kimpossible IG she has “If your not inventing you’re copying” she need fe start beat tings inna r dunce fren dem head
nothing about this funny not one shit about how can a great man such as Mr.Nelson Mandela weh help pave de way fe we as black ppl lead him country towards freedom nd free from most a de ignorance weh did a tek place after 27yrs in jail nd dis gurl dont know har history…de band wagon mentality weh sum a dem have nuh funny,dem see seh it a trend suh dem waan hop it but dont know de depth of it,this is no mistake from her she dont knw shit abt dis man nd neva find the honest time to…shame on you Sweets,goes to show how phucking empty yuh head actually is
good day met,metters,peepers nd others….
simplyyyyyyyyyyyyyyyyyyyyyyyyyy
No sah dem fe do BETTERRRR in a me Nicki Blacks voice – me shame n a no me e bad…..den if she dunno a who mek d speech somebody need fe sen a mecchez 2 har bout APARTHEID!!! PO TING!!
She we get the message one day inna barney’s, saks, nordstorm and all victoria secrets.
PO ting see wid them, a pure clout and boot and dance hall celebrity hype full up them head, them don’t even know them left foot different from the right, si the next man royal one Bobby over the next thread, a show her cheap looking ugly boot and claim say a 6g fi it, while white schowl a kill Daffy mother a Jamaica. Now look at that.
IS WHERE THIS UNEDUCATED FOOL COME FROM.
SHE NEED TO GO DEFLATE HER HER DAM BOTOX BIG HEAD AND PUT SOME SENCE INTO IT,
BECAUSE SHE DON,T EVEN QUALIFY TO BE A FOOL
I CANT BELIEVE THIS DANCE HALL DUNCE REALLY DID THIS TO HER SELF.
SHE COULD NEVER AND WILL NEVER BE AS IMPORTANT AS MR MANDELA
SHE A LOOK HYPE AND SO DAM DUNCE.
SHE MUST BE LONELY , THAT WHY SHE A WRITE SO MUCK F**KERY.
dat is a serious case of pretty dunce in full flight…..it sad bad!
133333333333333333333333333333333333333333 :peluk
cityyyyyyyyyyyyyyyyyyyy. what is happening maaa?
A wish sweet and dolly coulda knock dem head together and make sense… Cuz one brain Caah do fi one a Unuh you must share or get 2 each.
Bubblelikesoup
met longtime mi touch base. this bitch need beat with a bat all over har big lip and bleach out face, its just sad this girl have no clue about black history instead of buying all kind of bleaching cream run to the nearest bookstore and pick up some black history book u f**king duppy bat.
Mi head a boil…. Da gal ya disrespect… She want a somebody force
A something in har mouth fi straighten har brain to blood cloth…#hothead.
upset mi too. she is a f*kkin idiot and its not even cute.
She has noooo damn sense of the real world
people please teach your children, talk to them and give dem hugs everyday so they not as dunce and clueless as dis bleach out gyal
It is okay to make mistakes but honestly, if others identify your mistakes before you at all times, something is wrong. These girl haven’t been in school since they were like 16 &17 yrs old. I really feel bad for them. They both are not H.S grads neither do they have a GED..two stupid, dump ugly sister. I know them very well, I hope they open their eyes and see what’s going on in america. Without a degree, you ain’t going anywhere and you guys are not pretty so your looks ain’t going to take you anywhere either.
*the home where you are comming from also have a lot to do with your behavior. The mother is just the same and the older sister too. They all bleach and fake out themself too…I will be praying for them, they really need help..
ppl its a hoax….its been circulating on FB and IG since his passing….first they said Paris tweeted it but if you google it you will see its a hoax..dem a try mek Paris look duncer than she is lol